
In the finite element method, the domain of the problem is discretized into small elements.

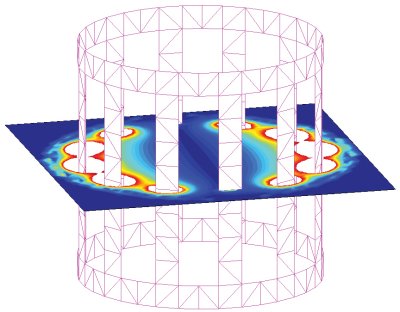
Stress analysis of waveguides and the combination of stress analysis with mode analysis are also reviewed. The chapter presents the FEM mode analysis of slab waveguides, rectangular waveguides, and optical fibers. FEM is also applicable to the stress analysis of optical waveguides. This chapter focuses on the finite element method (FEM), which is suitable for the mode analysis of optical waveguides having arbitrary refractive-index profiles and complicated waveguide structures. Katsunari Okamoto, in Fundamentals of Optical Waveguides (Second Edition), 2006 Publisher Summary As a result, the FEM has been implemented rigorously for solving a wide variety of problems in applied science and engineering and it has been rapidly developed over the years ( Rao, 2004).
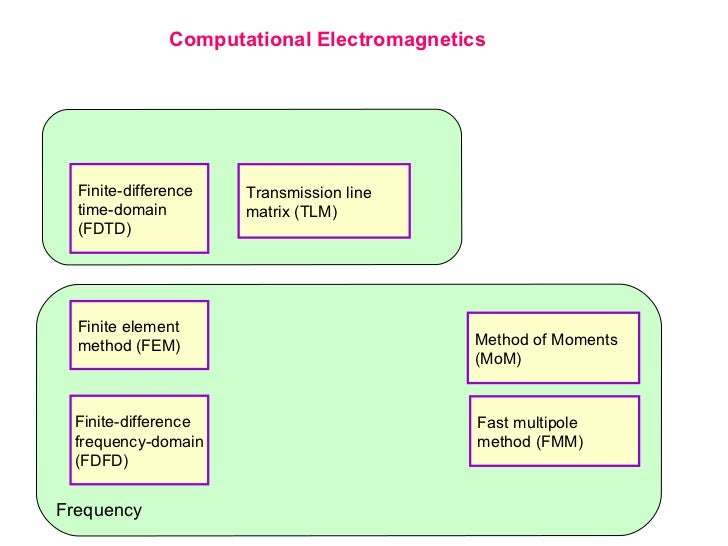
For convenience, the FEM procedure permits the continuum to be discretized into a finite number of parts (or elements) and emphasizes that the characteristics of the continuous domain may be estimated by assembling the similar properties of discretized elements per node. It is rightly addressed in Hutton (2004) that FEM is a computational technique used to obtain approximate solutions of boundary value problems in engineering. (1956), the application of finite elements has been presented for the analysis of aircraft structures and it is referred to as one of the key contributions in the development of the FEM. The concept of the Finite Element Method (FEM) was coined by Clough in the early 1960s in his infamous book entitled “ The finite element method in plane stress analysis”. Karan Kumar Pradhan, Snehashish Chakraverty, in Computational Structural Mechanics, 2019 4.1 Background


 0 kommentar(er)
0 kommentar(er)
